積分プログラム(台形積分) [fortran]

こんにちは、さくらえびです。
本稿では、台形積分に関するプログラムをご紹介します。
前回投稿した長方形微分に対し、
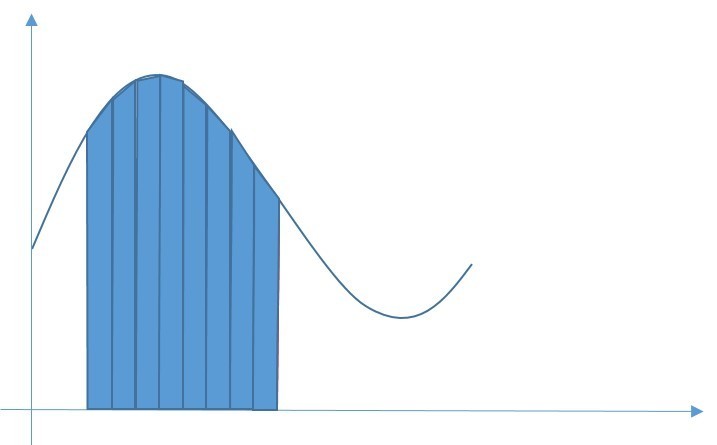
関数の傾きを直線で結んだ台形として、面積を計算する手法です。
関数が直線であれば、数値計算誤差はほぼ0となりますし、高次の関数だったとしても、長方形微分よりも、精度の良い積分結果を得られます。
式で書くと、こんな感じです。
\[
S = \int_a^b f(x)dx = \frac{(b-a)}{n} \sum_{i=1}^{n-1} \frac{f(x_i) + f(x_{i+1})}{2}
\]
図で描くと、こんな感じです。

プログラムは、

subroutine TRAP_INTEG(func,a,b,mesh,s)
implicit none
double precision func,a,b,s,s0,dx,pos
integer*4 mesh,i
s0 = 0.d0
pos = a
dx = (b-a)/dble(mesh)
do i=1,mesh-1
s0 = s0 + dx*(func(pos)+func(pos+dx))/2.d0
pos = pos+dx
enddo
s = s0
end subroutine

以下の実行プログラムを使用します。

program test
implicit none
external fx
double precision x0,x1,fx,s1,s2a,s2b,s2,s3
integer*4 mesh,i,num
num = 15
x0 = -1.d0
x1 = 1.d0
mesh = 10
do i = 1,9
call TRAP_INTEG(fx,x0,x1,mesh,s1)
call SQ_INTEG(fx,x0,x1,mesh,s2)
print *, "分割数,面積1,面積2,計算誤差,真値=",mesh,s1,s2,s1-s2,4.d0/3.d0
mesh = mesh*10
enddo
end program
function fx(x)
implicit none
double precision fx,x
fx = -x**2+1
end function

結果は以下のとおり、上に凸の関数なので、あまり違いが分かりにくいかと思います。