積分プログラム(台形積分)[C言語]
29/09/2023 15/10/2023
今回はプログラミングで最も基本的な積分方法である、台形積分の精度を評価してみます。
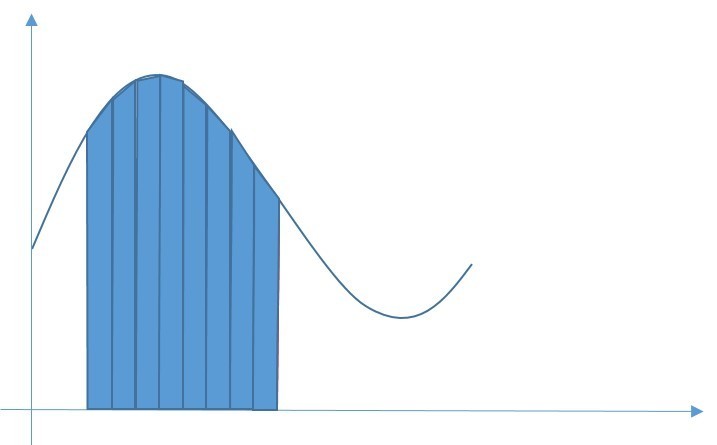
台形積分はまず、下図のように曲線を細かいdxで区切って、f(x)の値を算出します。
f(x)とf(x+dx)を台形の上底と下底とみなし、台形の面積を計算し、分割した領域を足し合わせていきます。
式で書くと、以下の通りです。
\[
S = \sum_{i=0}^{N} dx(f(x_{i}) + f(x_{i}+dx))/2
\]
台形積分は見てわかるように、曲線のカーブを直線で近似しているため、
分割数が荒いと、積分の数値計算精度が悪くなってしまいます。
C言語で行う場合のソースコードを以下に示します。
#include <stdio.h>
#include <math.h>
double fx1(double x1);
double INT_TRAP(double (*fun1)(double x),double xi,double xe,int mesh);
int main(void){
double x,xi,xe;
int mesh;
xi = 0.f;
xe = 1.f;
mesh = 10;
printf("Integral Result=%lf ,mesh = %d\n",INT_TRAP(fx1,xi,xe,mesh),mesh);
mesh = 100;
printf("Integral Result=%lf ,mesh = %d\n",INT_TRAP(fx1,xi,xe,mesh),mesh);
mesh = 1000;
printf("Integral Result=%lf ,mesh = %d\n",INT_TRAP(fx1,xi,xe,mesh),mesh);
mesh = 10000;
printf("Integral Result=%lf ,mesh = %d\n",INT_TRAP(fx1,xi,xe,mesh),mesh);
mesh = 100000;
printf("Integral Result=%lf ,mesh = %d\n",INT_TRAP(fx1,xi,xe,mesh),mesh);
mesh = 1000000;
printf("Integral Result=%lf ,mesh = %d\n",INT_TRAP(fx1,xi,xe,mesh),mesh);
return 0;
}
double fx1(double x1){
double fx1;
fx1 = x1*x1;
return fx1;
}
double INT_TRAP(double (*fun1)(double x1),double xi,double xe,int mesh){
double INT_TRAP;
double dx;
double S0;
double pos;
int id;
S0 = 0.f;
pos = xi;
dx = (xe-xi)/(double)mesh;
for (id = 1; id<= mesh-1;id= id + 1){
S0 = S0 + 0.5f*dx*(fun1(pos)+fun1(pos+dx));
pos = pos + dx;
}
INT_TRAP = S0;
return INT_TRAP;
}
計算結果を見てみます。結果はお分かりの通り、0.333333・・・が答えです。
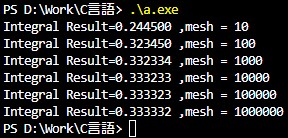
分割数を大きくすると、結構使えそうな精度が出てきましたが、分割数が多いということは、
処理数も大きいため、処理時間を短縮しないのであれば、使えそうな気がします。
by さくらえび
関連記事:
<積分関連>
・積分プログラム(台形積分) [fortran] — 思い立ったら作ってみる (y-fam.com)
・積分プログラム(台形積分) — 思い立ったら作ってみる (y-fam.com)