積分プログラム(台形積分)[python]
26/09/2022 15/10/2023
今回はプログラミングで最も基本的な積分方法である、台形積分の精度を評価してみます。
pythonで標準的に採用されている台形積分の精度を見てみたいと思います。
台形積分はまず、下図のように曲線を細かいdxで区切って、f(x)の値を算出します。
f(x)とf(x+dx)を台形の上底と下底とみなし、台形の面積を計算し、分割した領域を足し合わせていきます。
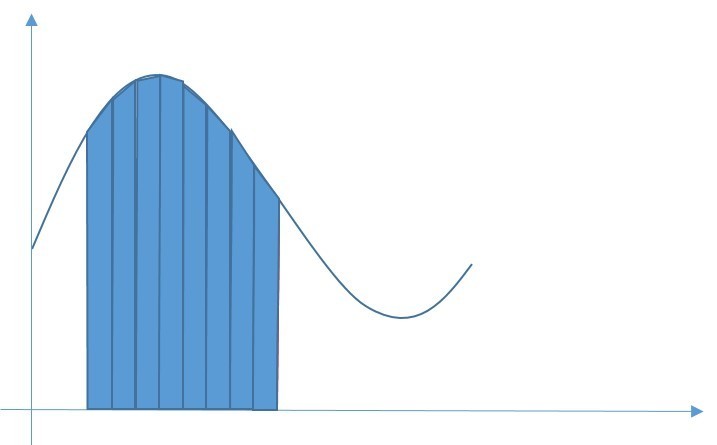
式で書くと、以下の通りです。
\[
S = \sum_{i=0}^{N} dx(f(x_{i}) + f(x_{i}+dx))/2
\]
台形積分は見てわかるように、曲線のカーブを直線で近似しているため、
分割数が荒いと、積分の数値計算精度が悪くなってしまいます。
pythonで行う場合、scipyライブラリにあるintegrateをインポートしておくと、
trapz関数として呼び出すことができます。
import math as mt
import scipy.integrate as si
import numpy as np
#積分(真値)
Int_t = (10**3)/3
#積分(10分割の台形積分)
x = np.linspace(0,10,10)
y = x**2
Int_1 = si.trapz(y,x)
error1 = Int_1 - (10**3)/3
#積分(100分割の台形積分)
x = np.linspace(0,10,100)
y = x**2
Int_2 = si.trapz(y,x)
error2 = Int_2 - (10**3)/3
#積分(1000分割の台形積分)
x = np.linspace(0,10,1000)
y = x**2
Int_3 = si.trapz(y,x)
error3 = Int_3 - (10**3)/3
#積分(10000分割の台形積分)
x = np.linspace(0,10,10000)
y = x**2
Int_4 = si.trapz(y,x)
error4 = Int_4 - (10**3)/3
#積分(分割をめっちゃ大きくしてみる台形積分)
x = np.linspace(0,10,100000000)
y = x**2
Int_5 = si.trapz(y,x)
error5 = Int_5 - (10**3)/3
#台形積分の値(10分割)
print("10分割の台形積分および誤差")
print(Int_1 , error1)
#台形積分の値(100分割)
print("100分割の台形積分および誤差")
print(Int_2 , error2)
#台形積分の値(1000分割)
print("1000分割の台形積分および誤差")
print(Int_3 , error3)
#台形積分の値(10000分割)
print("10000分割の台形積分および誤差")
print(Int_4 , error4)
#台形積分の値(100000000分割)
print("100000000分割の台形積分および誤差")
print(Int_5 , error5)
#真値
print("真値")
print(Int_t)
計算結果を見てみます。
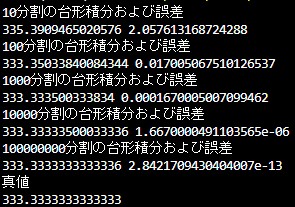
分割数を大きくすると、結構使えそうな精度が出てきましたが、分割数が多いということは、
処理数も大きいため、処理時間を短縮しないのであれば、使えそうな気がします。
by さくらえび
関連記事:
・積分プログラム(台形積分)[fortran]
・積分プログラム(長方形積分)[fortran]
・モンテカルロ積分 — 思い立ったら作ってみる (y-fam.com)