エルミート多項式 [C言語]

こんばんは　管理人のさくらえびです。
今日はエルミート多項式に挑戦。
エルミート多項式と言えば、調和振動子関数でもおなじみ(物理分野だとお馴染みのです。)
さっそく、MathJaxでスタイリッシュに書きましょう。
エルミート多項式は、以下の微分方程式を満たす多項式\(H_n(x)\)です。
\[
(\frac{d^2}{dx^2}-2x\frac{d}{dx}+2n)H_n(x) = 0
\]

ちなみに、TeX表記だといまのはこんな感じです。

(\frac{d^2}{dx^2}-2x\frac{d}{dx}+2n)H_n(x) = 0

さて、この微分方程式を解くと、下記のようなnごとの式表が出ます。
\(H_0(x)= 1\)
\(H_1(x)= 2x\)
\(H_2(x)= 4x^2-2\)
\(H_3(x)= 8x^3-12x\)
漸化式は、
\[
H_{n+1}(x) = 2xH_n(x) -2nH_{n-1}(x)
\]
なので、そろそろソースコード
C言語：

double Hermite(int node, double x){
double Hnx;
double tmpH,tmp1,tmp2;
if(node == 0){
Hnx = 1.0;
}else if(node == 1){
Hnx = 2*x;
}else{
tmpH = 1;
tmp1 = 2*x;
for(int i=1;i <=node-1;i++){
tmp2 = tmp1;
tmp1 = 2*x*tmp1 - 2*i*tmpH;
tmpH = tmp2;
}
Hnx = tmp1;
}
return Hnx;
}

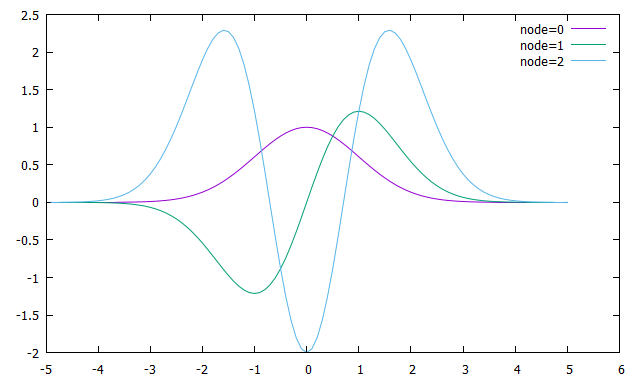
結果は同じなので、最後にノード2までのグラフを載せておきます。
ちなみに、グラフ外に飛んでいくのが好きじゃないので、\(exp(-x^2/2)\)を掛けています。