ニュートン・ラフソン法 [C言語]

こんにちは　さくらえびです。
今日はニュートン・ラフソン法のC言語での組み方をご説明します。
ニュートン・ラフソン法は求根アルゴリズムの一つで、簡単に説明すると、
\(f(x)=0\)となる\(x\)を求める方法です。
しかし、根(解)が複数ある場合、最近接の解が適用されます。
なので、解がどこにあるのかわからないものに対して適用するには、難しい方法です。
ニュートン・ラフソン法の求根式は以下のとおりです。
\[
x_{n+1} = x_n – f(x_n)/f'(x_n)
\]
\(x_n\)は最初、\(x_0\)から始まり、\(\lim_{n \to \infty} x_n\)で収束します。
とはいえ、無限までプログラムを実行し続けるわけにはいかないので、
収束したと認めるための閾値が必要となります。
ソースコードを下記に示します。
まずニュートン・ラフソン法の関数定義は、ポインタを使用して下記のように定義します。

double NEW_LAP(double(*fun)(double x),double x_ini);

定義したNEW_LAP関数の内部処理は、下記のとおりです。

double NEW_LAP(double(*fun)(double x),double x_ini){
double x_new;
double x_old;
x_new = x_ini;
while(fabs(x_new - x_old) >= 0.000001){
x_old = x_new;
x_new = x_old - fun(x_old)/DIF_F(fun,x_old);
}
return x_new;
}

関数の微分プログラムは前回作成のものを使っています。
では、関数\(f(x)=x^2 – 1\)に対して、ニュートン・ラフソン法を適用するプログラムのテストをします。
下記はテスト用のソースコードです。

#include 
#include 
double DIF_F(double (*fun)(double x),double xd);
double fx(double x);
double NEW_LAP(double(*fun)(double x),double x_ini);
int main(void){
double x;
x = 1.0;
printf("%lf,%lf,%lf",fx(1.0),NEW_LAP(fx,-2.0),DIF_F(fx,1.0));
return 0;
}
double fx(double x){
double fx;
fx = pow(x,2.0)-1.0;
return fx;
}

結果は下記のとおりです。おおよそ出収束しているようです。

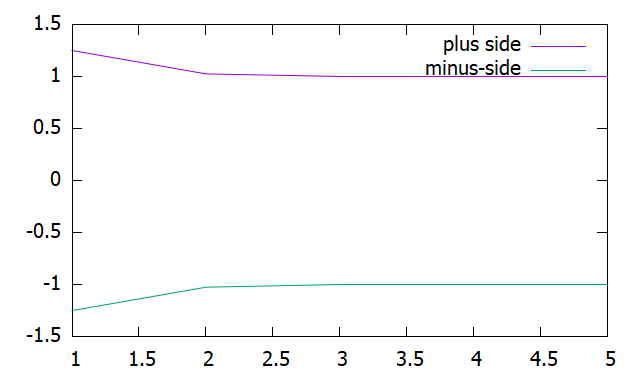
下記は収束までの値を示した図です。

by さくらえび