ロピタルの定理 [C言語]
25/03/2019
こんにちは。さくらえびです。
本稿では、C言語版のロピタルの定理について、紹介します。
ロピタルの定理は、数値計算をする上で、零点近傍での処理に有用です。
たとえば、分母分子ともに0もしくは±∞に発散する関数を0点を用いて積分する場合などは、
零点での計算で、収束させることが可能です。
しかしながら、0のみを扱うと、問題が生じます。
数値計算において、完全な0が発生しないことが多々あるからです。
この場合、\(10^-10\)は0であると定義してあげることで、0を作り出すことが可能です。
では、定義式です。
\[
f(0)/g(0) = \lim_{x \to 0} f'(x)/g'(x)
\]
では、C言語でのソースコードを紹介します。
double L_HOP(double (*fun1)(double x1),double (*fun2)(double x2)){
double L_HOP;
L_HOP = DIF_F(fun1,0.0)/DIF_F(fun2,0.0);
return L_HOP;
}
ここで使われている関数 DIF_F(fun,x)については、下記ページを参考にしてください。
微分プログラム[C言語]
テストはわかりやすい関数
\[
f(x) = sin(2x)
\]
\[
g(x) =x + sin(x)
\]
について、処理を行います。テストコードは下記のとおりです。
#include <stdio.h>
#include <math.h>
double DIF_F(double (*fun)(double x),double xd);
double L_HOP(double (*fun1)(double x1),double (*fun2)(double x2));
double fx1(double x1);
double fx2(double x2);
int main(void){
double x;
printf("f(0)/g(0)=%lf\n",L_HOP(fx1,fx2));
return 0;
}
double fx1(double x1){
double fx1;
fx1 = sin(2.0*x1);
return fx1;
}
double fx2(double x2){
double fx2;
fx2 = x2 + sin(x2);
return fx2;
}
結果は下記のとおりとなっています。期待値は1ですので、この処理は成功しています。
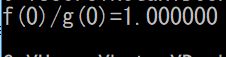
このように、C言語でも関数を引数にすることで、ロピタルの定理を実装することができました。
by さくらえび