差分法 前進・後退・中心[fortran]
23/10/2019 30/09/2023
本項では差分法について紹介します。
差分法とは、つまり微分をプログラム上で行う上で必要な手法となります。
微分の公式は下記のとおり、よく知られたものです。
\[
f'(x) =\lim_{h \to 0} \frac{f(x+h)-f(x)}{x+h-x}
\]
このとき、プログラム化すると、このようになります
これはタイトルでも記載したとおり、前進法と言います。
次に後退法ですが、x-hからxに対して前進法を行ったものと同値となります。(証明はまた別の記事にてご紹介します。)
式にすると、下記のとおりです。
\[
f'(x) =\lim_{h \to 0} \frac{f(x)-f(x-h)}{x-x+h}
\]
上記2つの式の結果が一致していることを利用し、2つの式を足して両辺を2で割ると、下記の式を得ることができます。
\[
f'(x) =\lim_{h \to 0} \frac{f(x+h)-f(x-h)}{2h}
\]
これが中心差分の式となります。
ではそれぞれをfunctionにして実行してみましょう。
ソースコードは下記
program main
implicit none
external test
double precision test,C_DIFF,F_DIFF,B_DIFF
double precision x,dx
integer*4 id
dx = 1.0E-7
do id = 1,10
x = dble(id-1)*0.1
print *, 'F_DIFF , Error',F_DIFF(test,x,dx),F_DIFF(test,x,dx)-2.d0*x+1
end do
do id = 1,10
x = dble(id-1)*0.1
print *, 'B_DIFF , Error',B_DIFF(test,x,dx),B_DIFF(test,x,dx)-2.d0*x+1
end do
do id = 1,10
x = dble(id-1)*0.1
print *, 'C_DIFF , Error',C_DIFF(test,x,dx),C_DIFF(test,x,dx)-2.d0*x+1
end do
end program
function test(x)
implicit none
double precision test,x
test = x**2.d0 - x + 2
end function
function C_DIFF(fun,x,dx)
external fun
double precision fun,x,dx
double precision F_DIFF,B_DIFF,C_DIFF
C_DIFF = 0.5d0*(F_DIFF(fun,x,dx)+B_DIFF(fun,x,dx))
end function
function F_DIFF(fun,x,dx)
implicit none
double precision F_DIFF,fun,x,dx
F_DIFF = (fun(x+dx)-fun(x))/dx
end function
function B_DIFF(fun,x,dx)
implicit none
double precision B_DIFF,fun,x,dx
B_DIFF = (fun(x)-fun(x-dx))/dx
end function
計算結果は下記
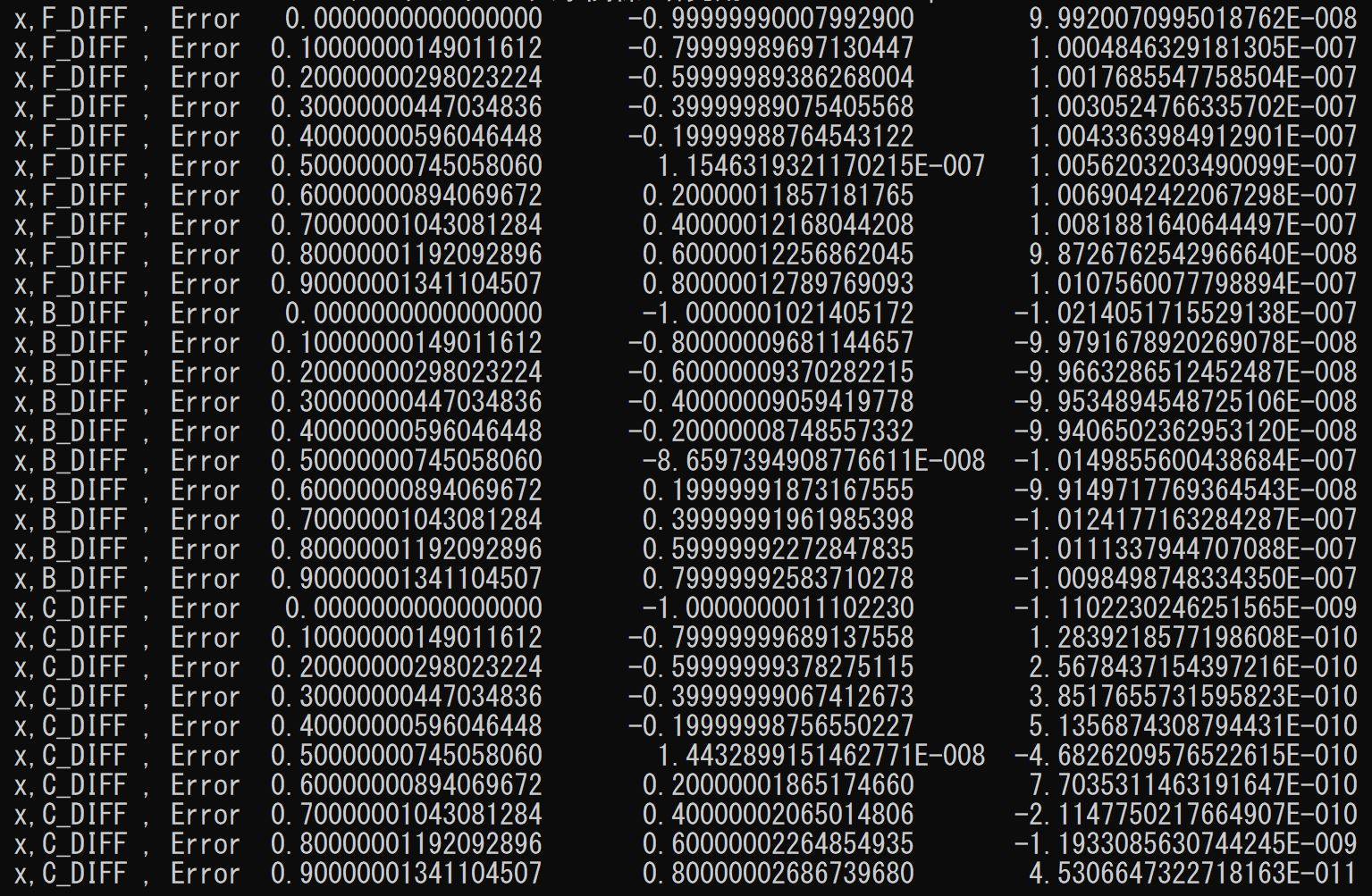
ただし、後退差分は、極座標系の動径方向では0点において使用できないため、ロピタルの定理などで0点を決定する際は前進差分が必要となります。
Reference
[1]T.TAGUCHI技術評論社 Fortranハンドブック」(2015)