ラゲール多項式[fortran]
本稿では、ラゲール多項式について説明します。ラゲール多項式は、微分方程式
\[
\bigl( x \frac{d^2}{dx^2} + (1-x) \frac{d}{dx} + n \bigr)L_n(x) = 0
\]
の解となる多項式です。記号で書くと、\(L_n(x)\)と書きます。
ラゲール多項式は、下記条件を満たします。定義は諸説ありますが、今回は[2]を参照しています。
1:漸化式
\[
L_{n+1}(x) = (2n + 1 -x)L_n(x) – n^2L_{n-1}(x)
\]
2:直交性
\[
\int_0^\infty dxL_n(x)L_m(x) \mathrm{e}^{-x}= \delta_{nm}(n!)
\]
では、作成したソースコードを条件1(漸化式)を満たすように作成します。
その後、直交性と微分方程式を満たしていることを確認します。
まずは、直交性。半無限積分のため、ガウス・ラゲールの求積法 [1] を用います。
ガウス・ラゲールの求積法については、別途記事を作成します。
ラゲールの多項式のファンクションソースコード
function Ln(n,x)
implicit none
double precision Ln,x,L0,L1,L2
integer*4 n,id
if (n ==0) then
Ln = 1.d0
return
endif
if (n == 1) then
Ln = -x + 1.d0
return
endif
if (n >= 2) then
L0 = 1.d0
L1 = -x + 1.d0
do id = 2,n
L2 = (2.d0*(id-1)+1-x)*L1 - dble((id-1)*(id-1))*L0
L0 = L1
L1 = L2
enddo
Ln = L2
return
endif
end function
積分結果

n=mの時の積分値 
n≠mの時の積分値
次に、微分方程式の解となっていることを確認します。
これは実は手で解けるので、あまり計算機的に解くのはお勧めしませんが、
値が確かであることを確認するためであれば、計算機的に解くことは問題ありません
微分方程式への代入結果
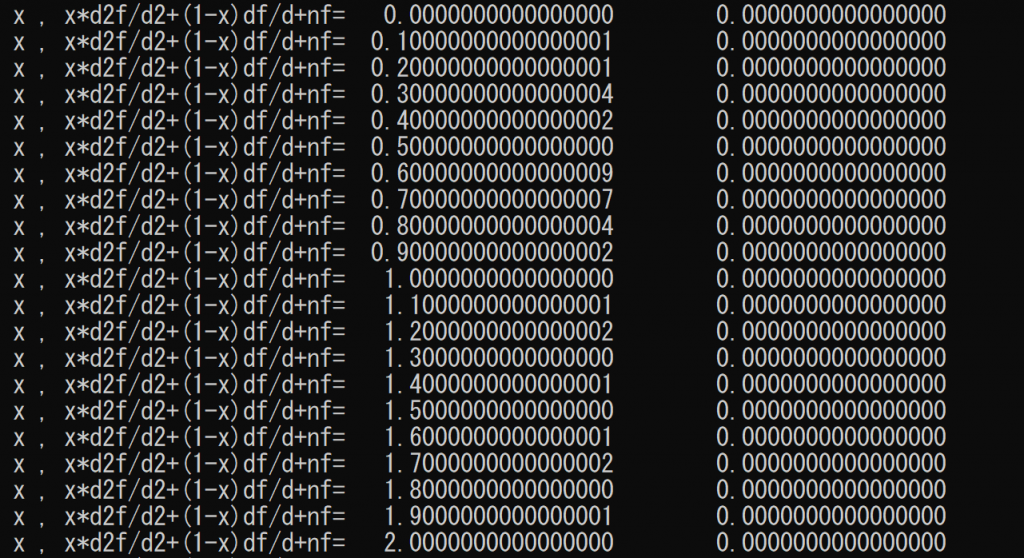
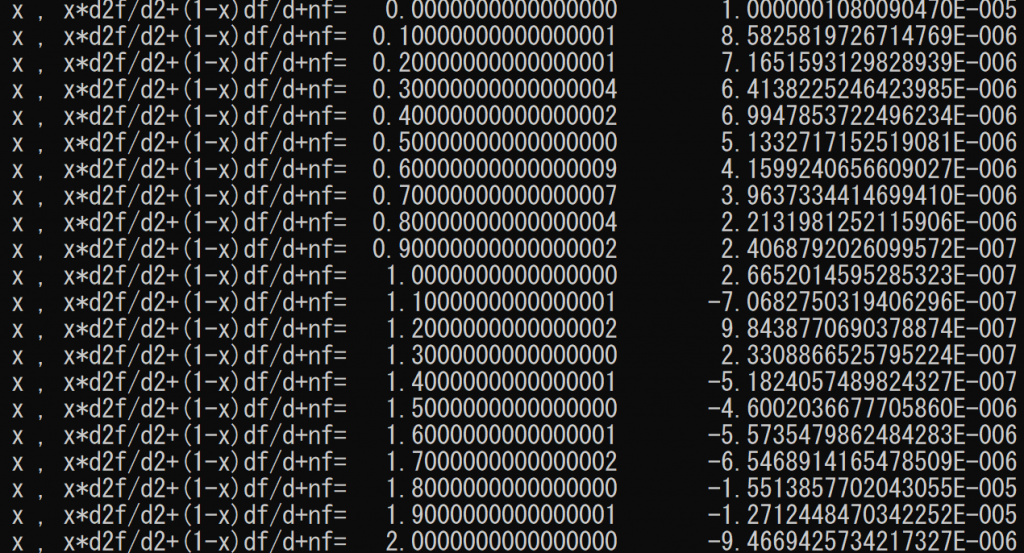
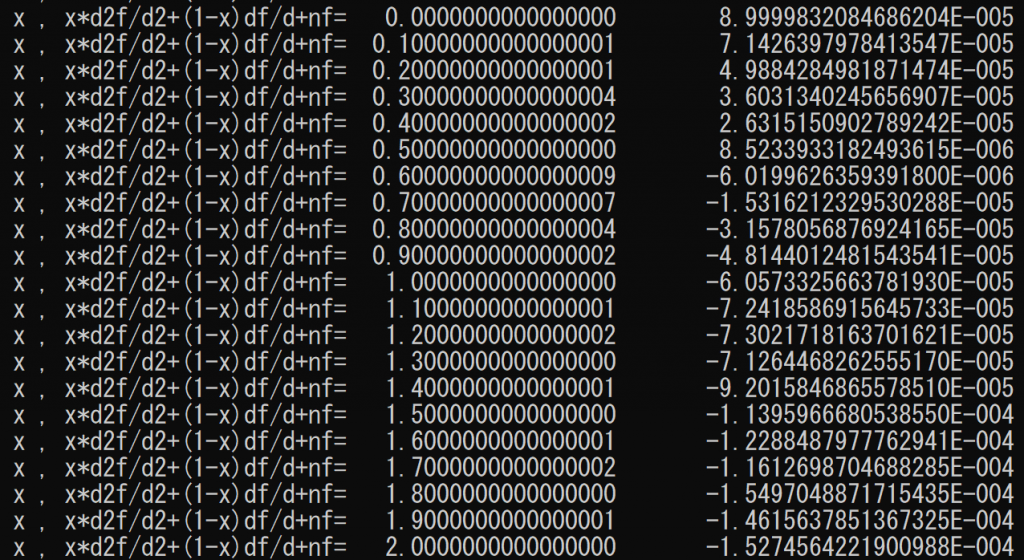
n=3のときの微分方程式の値(0近くに減衰しているのでおおむね正しいが、誤差は差分によるもの)
このように、ラゲール多項式が微分方程式の解となり、直交性を満たすことが確認できました。
[1] T.TAGUCHI 技術評論社 Fortranハンドブック」(2015)
[2] S.MORIGUCHI et. al. 岩波書店「特殊函数 岩波 数学公式3」(1987).
[3] S.OKABE 近代科学社 「量子論 運動と方法 シミュレーション物理学5」(1992).