ラゲールの陪多項式[fortran]
本稿では、ラゲールの陪多項式について、説明します。
ラゲールの陪多項式は下記微分方程式を満たす多項式です。
\[
\bigl( x \frac{d^{k+2}}{dx^{k+2}} + (1+k-x) \frac{d}{dx} + (n-k) \bigr)L^k_n(x) = 0
\]
の解となる多項式です。記号で書くと、\(L^k_n(x)\)と書きます。
ラゲール多項式は、下記条件を満たします。定義は諸説ありますが、[1-2]を参照しています。
1:漸化式
\[
(n+1)L^k_{n+1}(x) = (2n + k + 1 -x)L_n(x) – (n+k)2L^k_{n-1}(x)
\]
2:微分式その1
\[
x\frac{d}{dx}L^k_n(x) = nL^k_n(x) – (n+k)L^k_n(x)
\]
3:微分式その2
漸化式の結果を用いて、微分式を再度記述すると、下記のように記述でき、ノード(n-1)を扱わずに済む。
これは、数値計算を行う上で、とてもありがたいことです[3]。
\[
x\frac{d}{dx}L^k_n(x) = (n+1)L^k_n(x) -(n+k+1-x)L^k_n(x)
\]
4:直交性
\[
\int_0^\infty dx
x^k L^k_n(x)L^k_m(x) \mathrm{e}^{-x} = \delta_{nm}(\frac{\Gamma(n+k+1)}{\Gamma(n+1)})
\]
ノルムの部分はガンマ関数です。ガンマ関数は、その値が整数の時、(引数-1)!と等価を意味します。
今回は整数を取り扱っているので、これで構いません。ただし、球対称の調和振動子Schrödinger方程式を解いた時の解は、\( k = l_\alpha + 1/2 \)が現れるため、n+1/2のガンマ関数の計算をする必要があります。
では、作成したソースコードを条件1(漸化式)を満たすように作成します。
その後、直交性と微分方程式を満たしていることを確認します。
ラゲールの陪多項式のファンクションソースコード
function Lnk(n,k,x)
implicit none
double precision Lnk,x,k
integer*4 n,i
double precision Lnk0,Lnk1,Lnk2
if(n == 0) then
Lnk = 1.d0
else if(n == 1) then
Lnk = 1.d0 + k - x
else
Lnk0 = 1.d0
Lnk1 = 1.d0 + k - x
do i = 2,n,1
Lnk2 = Lnk1
Lnk1 = -((x-2.d0*dble(i)- k + 1.d0)*Lnk1+(dble(i)+k-1.d0)*Lnk0)/dble(i)
Lnk0 = Lnk2
enddo
Lnk = Lnk1
endif
end function Lnk
積分結果(直交性の確認)半無限積分のため、ガウス・ラゲールの求積法を使用します[4]。
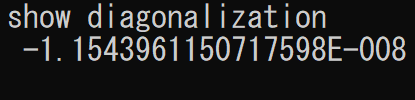
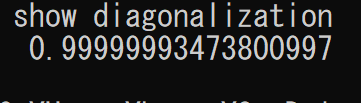
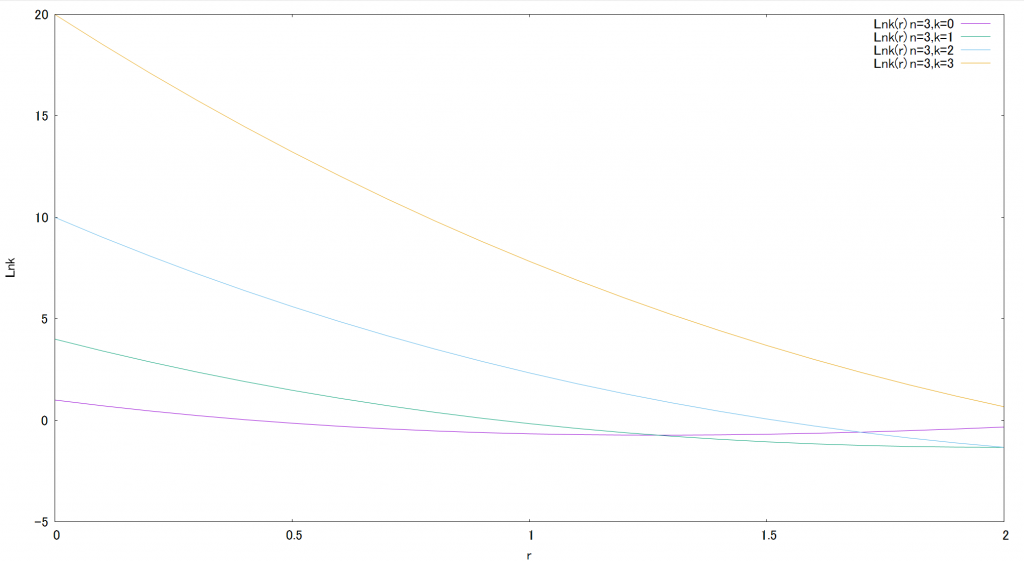
グラフ(ラゲール陪多項式の計算値)
グラフ(ラゲール陪多項式の計算値に\( \mathrm{e}^{-x} \)をかけたもの)
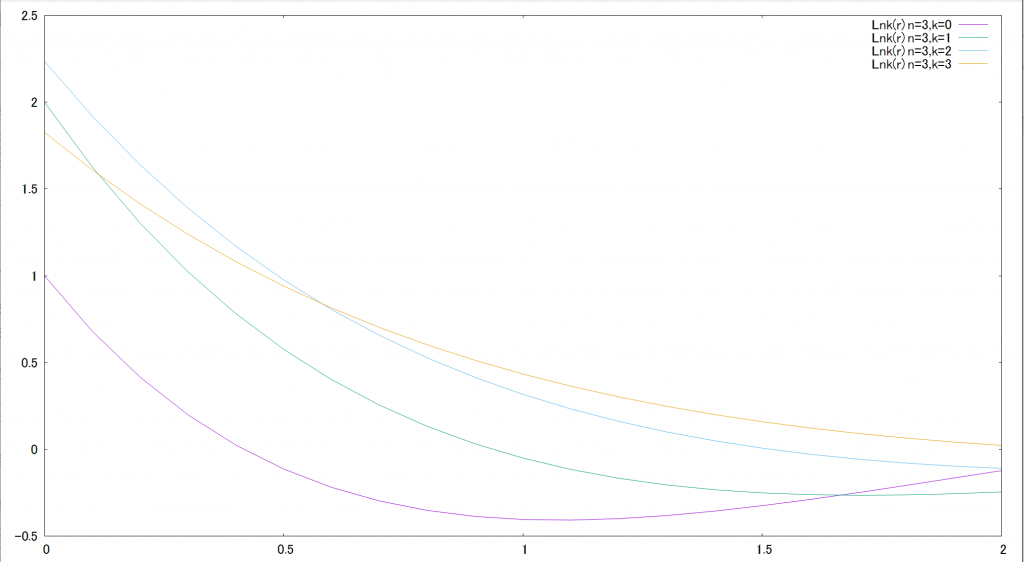
\mathrm{e}^{-x} \)
本稿では、ラゲールの陪多項式について、記載しました。
Reference
[1] S.OKABE「量子論 運動と方法 シミュレーション物理学5」近代科学社(1992).
[2] S.MORIGUCHI et. al.「特殊函数 岩波 数学公式3」岩波書店(1987).
[3] M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions (Dover, New York, 1965).
[4] T.TAGUCHI Fortranハンドブック」技術評論社(2015)