COVID-19を機に学ぶSIRモデル
こんにちは。さくらえびです。
今回は新型コロナウイルス(COVID-19)の感染拡大を期に、SIRモデルを学びたいと思います。
まずは、用語を理解してみたいと思います。
・SIRモデルのSは感受性保持者。なるほど、専門外なので意味がわかりません。英語で読むとSusceptible
z引き受けやすいという意味です。つまり抗体を持たない人と解釈して良さそうです。
・SIRモデルのIは感染者(Infected)これはわかる!筆者でもこれはわかる!!
・SIRモデルのRは免疫保持者(Recover)とか隔離者(Remove)と訳されています。
引っかかるけど受け止めましょう。
では数式を見ていきます。シミュレーションしたいのでここからが大事です。
Susceptible(感受性保持者)の差分項
\[
\frac{dS}{dt} = – \beta S(t)I(t)
\]
Infected(感染者)の差分項
\[
\frac{dI}{dt} = \beta S(t)I(t) – \gamma I(t)
\]
Recover(免疫保持者)またはRemove(隔離者)
\[
\frac{dR}{dt} = \gamma I(t)
\]
束縛条件
\[
S(t) + I(t) + R(t) = Constant
\]
連立微分方程式と束縛条件を把握できました。微分は1日ずつの前進オイラー法(過去記事)でなんとかできそうです。
早速ソースコードに移します。
program SIR_SIM
implicit none
double precision Sfun(1000),Ifun(1000),Rfun(1000)
double precision beta,gamma1,gamma,beta1,TOT,inf,dead
integer*4 day,past
beta1 = 0.0000000017d0
dead = 0
gamma = 1.d0/14.d0
past = 90
Ifun(1) = 1
inf = Ifun(1)
Sfun(1) = 124999999
Rfun(1) = 0
print *, 1,Sfun(1),Ifun(1),Rfun(1),0
do day = 2,600
Sfun(day) = Sfun(day-1) - beta1*Ifun(day-1)*Sfun(day-1)
Ifun(day) = Ifun(day-1) + (beta1*Sfun(day-1)-gamma)*Ifun(day-1)
Rfun(day) = Rfun(day-1) + gamma*Ifun(day-1)
TOT = Sfun(day)+Ifun(day)+Rfun(day)
print *, day,Sfun(day),Ifun(day),Rfun(day),Ifun(day) - Ifun(day-1),TOT
enddo
end program
結果を確認します。
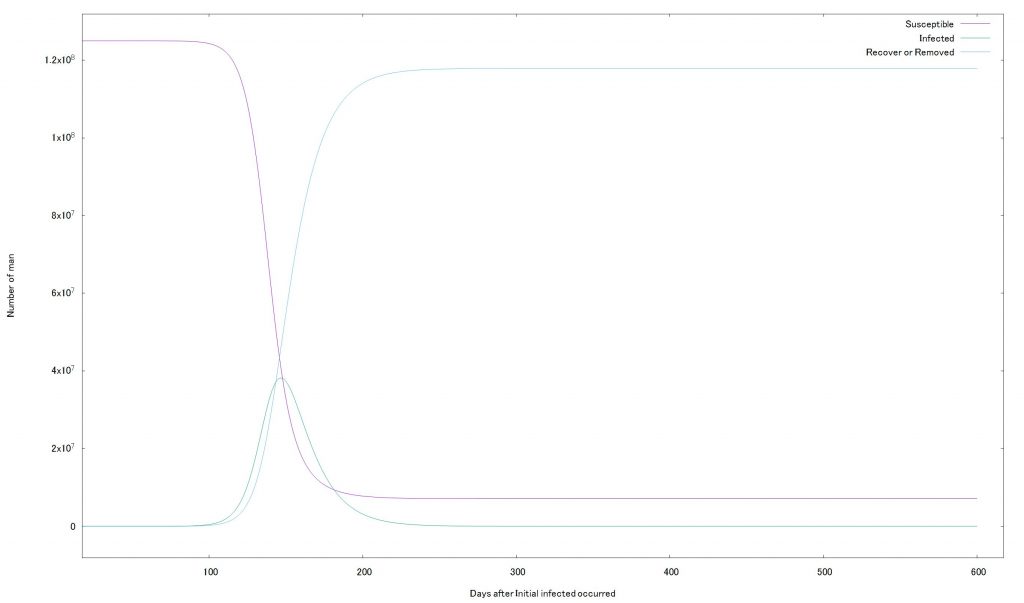
うん、書籍どおりの結果が出ました。緊急事態宣言前に北大の先生が言っていた「このままでは1ヶ月後には〜人の感染者が発生する」という言葉は理解できますね。
4月7日に発表した緊急事態宣言も計算の中に入れてみましょう。SIRモデルのうち、γを操作します。γの逆数は、回復までの平均日数14日間とおきますが、これは隔離率と置き換えられるため、緊急事態宣言下ではこの値を大きくしてみます。
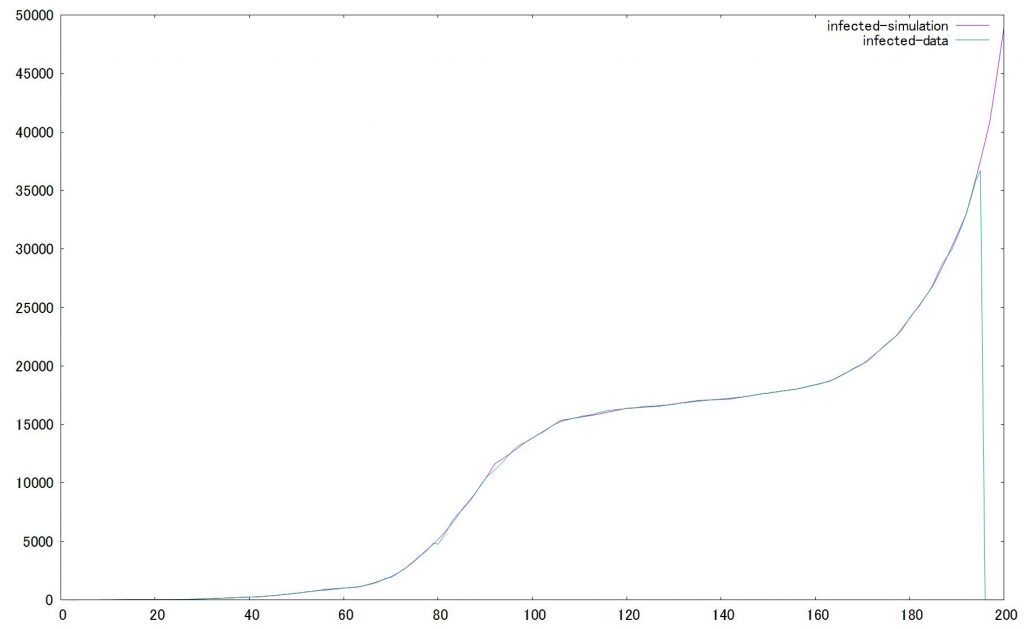
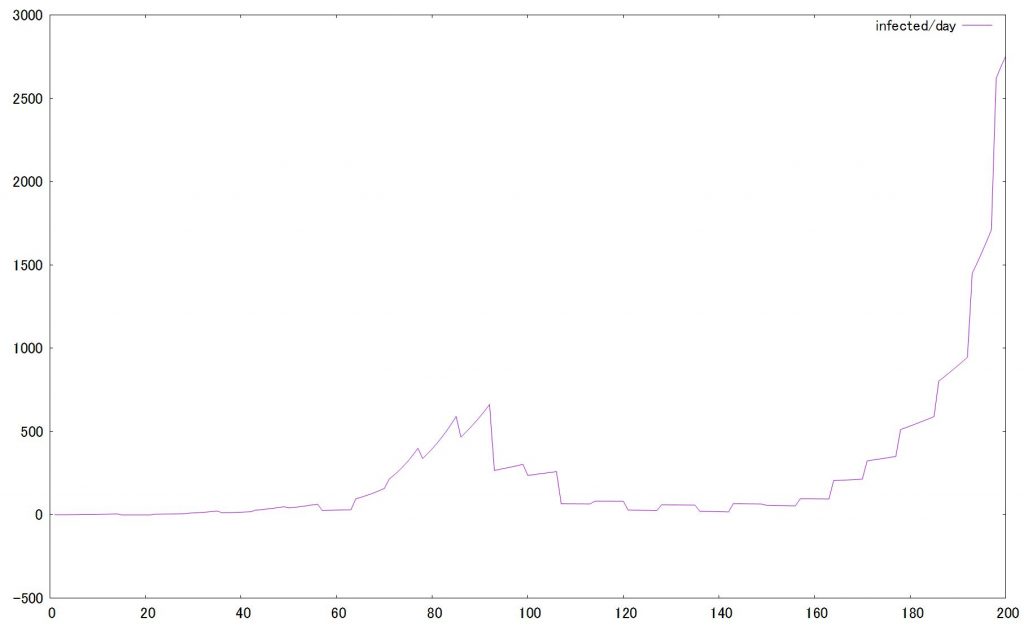
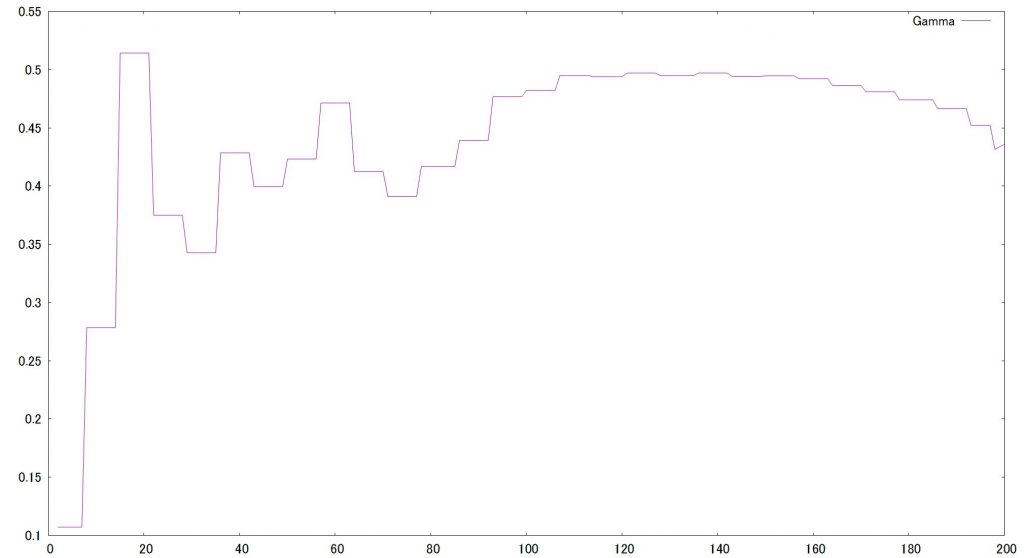
この計算式、エンデミックには対応していません。なぜならこの計算、Recoverした人はもう感染しない前提だからです。今回の、COVID-19は一度感染した人も感染してます。バッチ処理入れてみたいですね。検討の余地ありです。
いかがでしたでしょうか?シミュレーションしてみると、ニュースでよく見るグラフが身近に感じられますね。でも身近だと困るのでソーシャルディスタンスを確保しましょう!
次回はSIRモデルを改造してみたいと思います。
[1]「自然の数理と社会の数理 2」 佐藤總夫 日本評論社(1984)
[2]「感染症の数理モデル」 稲葉寿 培風館(2008)
by さくらえび