ルジャンドル多項式 [fortran]

こんにちは　さくらえびです。
本稿は、ルジャンドル多項式についてご説明します。
定義は、ルジャンドル微分方程式を満たすルジャンドル関数のうち、非負整数に当たるものを指します。
ルジャンドル微分方程式は下記のとおりです。
\[
\frac{d}{dx} \bigl[ (1-x^2)\frac{d}{dx}f(x) \bigr] + \lambda ( \lambda + 1)f(x) = 0
\]
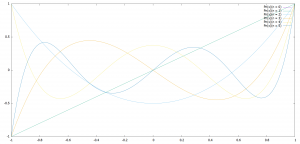
これを満たすルジャンドル関数のうち、非負整数\((\lambda = 0,1,2,3…)\)のものをルジャンドル多項式と言います。
ロドリゲス公式によれば、下記のように書けます。
\[
P_n (x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} \bigl[ (x^2-1)^n \bigr]
\]
ただし、今回はプログラムにするので、帰納的に扱えるボネの漸化式を適用します。
\(P_0 (x) = 1 , P_1 (x) = x \)として、下記の漸化式からn ≧ 2における \( P_n (x) \)を求めます。
\[
P_{n+1} = \frac{(2n+1)xP_n (x) – nP_{n-1}(x) }{(n+1)}
\]
では、関数のソースコードです。

function Pnx(n,x)
implicit none
double precision Pnx,x,tpnx,tpnx0,tpnx1
integer*4 n,id
if (n == 0) then
Pnx = 1
elseif (n == 1) then
Pnx = x
else
tpnx0 = 1
tpnx1 = x
do id=2,n
tpnx = ((2.d0*dble(id)-1.d0)*x*tpnx1 - dble(id-1)*tpnx0)/dble(id)
tpnx0 = tpnx1
tpnx1 = tpnx
enddo
Pnx = tpnx
endif
end function

結果は、下記図のとおりです。数表を見る限りでも、計算できているようです。
by さくらえび