第2種完全楕円積分 [fortran]

こんにちは　管理人のさくらえびです。
今日は、第二種完全楕円積分のプログラムを紹介します。
英語で言うと、
complete elliptic Integral of the 2nd kind
・
・
・
はい、どうでもいいですね(笑)
さて、まずは数式のご紹介
下記定積分を第2種完全楕円積分と言います。
\[
E(k) = \int_0^\frac{\pi}{2} (1-k^2sin^2\theta)^{1/2} d\theta
\]
プログラムしやすい式に書き直すと、
\[
E(k) = \frac{\pi}{2}\sum_{n=0}^\infty \bigl(\frac{(2n-1)!!}{(2n)!!} \bigr)^2 (\frac{k^{2n}}{(1-2n)})
\]
こんな感じ。
でも、収束するまで時間がかかるので、
\[
　\kappa = \frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}}
\]
と、ベキ級数にしてしまえば、
\[
E(k) = \frac{\pi}{2(1+\kappa)}\bigl[1+\sum_{n=0}^\infty \frac{(2n-3)!!}{(2n)!!}\kappa^{2n}\bigr]
\]
こんな感じです。
このプログラミングは下記のとおりです。

function ELLIP2nd(x,endT)
!*----------------------------------------------------
!   This function is derive complete Elliptic Integral of 2nd kind
!-----------------------------------------------------
!definision valiables
    implicit none
    double precision ,parameter :: pi = 3.141592653589793d0
    double precision ELLIPE,tempE
    double precision x,xx,nFac,CC,CCE
    integer*4 i,endT
    xx = (1.d0-dsqrt(1-x*x))/(1.d0+dsqrt(1-x*x))
    CCE = pi*0.5d0/(1.d0+xx)
    tempE = 1
    do i = 1 ,endT
      CC = (nFAC(2,2*(i-1)-3)/nFAC(2,2*(i-1)))**2
      tempE = tempE + CC*(xx**(2*(i-1)))
    enddo
    ELLIP2nd = CCE*tempE
end function ELLIP2nd

結果は下記のとおり

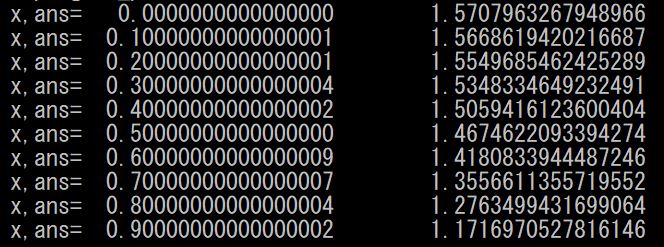
ではでは

さくらえび